Yeah, we can move on to continue this Marathon…
Solution of problem 17:
Any three distinct non-collinear points lie on an unique plane.
This statement means that if we have three points not on one line, then only one specific plane can go through those points. The plane is determined by the three points because the points show us exactly where the plane is.
So, it doesn’t even matter that, these points are in which dimensional space.
Now, consider, M is the midpoint of BC.
In \triangle ABM and \triangle ACM,
\angle ABM = \angle ACM [ given that, \angle ABC = \angle ACB]
AM = AM
BM = CM
So, \triangle ABM \cong \triangle ACM.
AB = AC . [Proved]
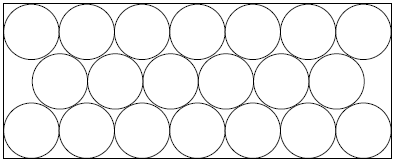
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as \frac{1}{2}(\sqrt{p}-q) where p and q are positive integers. Find p+q.(Problem 18)
Source: 2002 AIME
Solution of Problem 18:
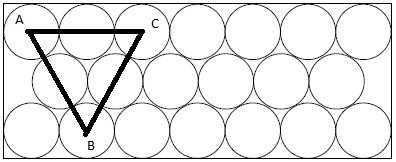
Suppose, the radius of every circle is x. So the length of the longer dimension is 14x.
In the figure, ABC is an equilateral triangle. The length of it’s side is 4x.
The area of \triangle{ABC} = \cfrac{\sqrt{3}*{(4x)}^2}{4}=4x^2\sqrt3
The height of \triangle{ABC} = 2*\cfrac{4x^2\sqrt3}{4x} = 2x\sqrt3
The length of the shorter dimension is 2x\sqrt3+2x = 2x(\sqrt3 +1).
The ratio of the longer dimension of the rectangle to the shorter dimension = \cfrac{14x}{2x(\sqrt3+1)}= \cfrac{7}{\sqrt3+1}=\cfrac{7}{\sqrt3+1}* \cfrac{\sqrt3-1}{\sqrt3-1}=\cfrac{7\sqrt3 - 7}{3-1}=\cfrac{1}{2}(\sqrt{147} - 7)
Here, p=147 , q= 7
\therefore p+q=147+7=154 \fbox{Ans}
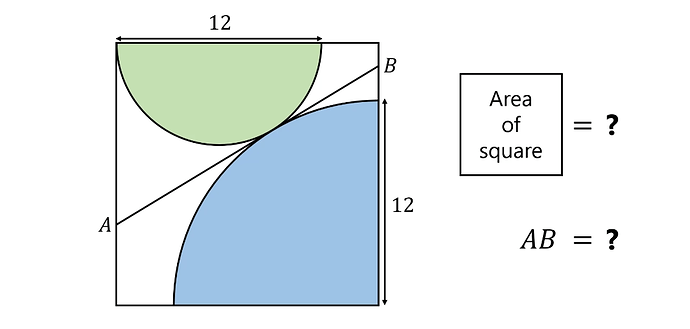
AB=18
Amd I think the area is (3+3×17^½)²
Please prove it and write a reply.
Ok I will prove it when I get time
Can you please post the next problem?
Somebody, please post a new problem…
I have solved it!!. It is a fun geometry problem. But the process is bit messier
তোমার সমাধান হয়েছে বললে তো হবে না, তোমার সেটা আপলোড করতে হবে, এইটাই ম্যারাথনের নিয়ম।
Can you please post the next problem?(It will be problem 21)
Pro @marzuqcesc a real pro
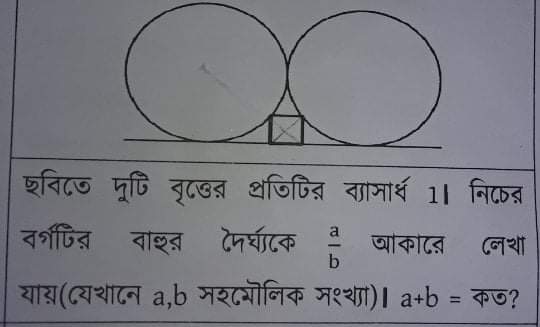
Problem 21
In the figure, two unit(radius 1) circle are externally tangent. A square is touching both the circle and their common tangent. If the square side length is \frac{a}{b} then what is a+b ?
Question source
Bdmo প্রস্তুতি
Why nobody solved it?
আমি noob তাই আমি পারি না
Someone, please post a new problem…