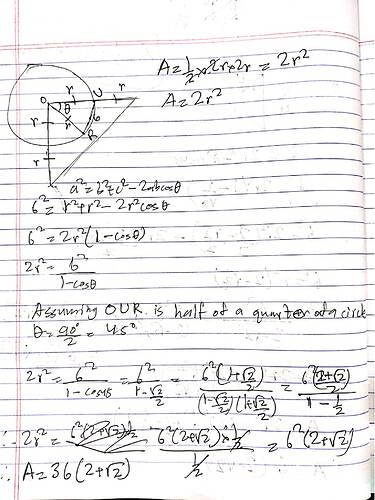Math Olympiad Marathon

[ferojkabirnh9]

Problem 1

1. Reply only answer or solution
2. All can send me any category questions privately I will post it here

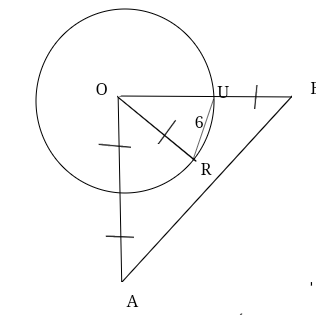
In the picture AO=BO And \frac {1}{2}AO=\frac{1}{2}BO
RU=6, So what is the area of \triangle{AOB} ?

Last date of replying answer is 03/03/2023 at 9:00 a.m

Ans will given in 5hat day also

[wasifullah_1]

[nargisakter1572]

In the question, you have to tell the area of \triangle{AOB}. NOT ''A''.

[ferojkabirnh9]

ক্ষেত্রফল বের করতে হবে

[nargisakter1572]

\fbox{You are right.}

[nargisakter1572]

That's right.

[ferojkabirnh9]

Problem 2

\fbox{You should give the full process}

1000^n+283+928+2000n+500 কে 1000 দ্বারা ভাগ করলে ভাগশেষ কত থাকবে ?

Last date of posting answer is 06/03/2023 at
12:00 p.m.

[Arko_1729]

প্রদত্ত রাশিতে প্রথম ও চতুর্থ রাশি 1000^n ও 2000n, 1000 দ্বারা বিভাজ্য। সুতরাং 283+928+500 কে 1000 দিয়ে ভাগ দিলে যত ভাগশেষ থাকে তাই উত্তর।
283+928+500=1711 কে 1000 দিয়ে ভাগ দিলে ভাগশেষ 711
নির্ণেয় উত্তর 711

[wasifullah_1]

By A I meant area, but it seems like I was wrong.

[nargisakter1572]

\fbox{Oh!!!!! I see}

[ferojkabirnh9]

Your answer is correct.

[ferojkabirnh9]

Problem 2
Solution

প্রদত্ত রাশিতে প্রথম ও চতুর্থ রাশি 1000^n ও 2000n, 1000 দ্বারা বিভাজ্য। সুতরাং 283+928+500 কে 1000 দিয়ে ভাগ দিলে যত ভাগশেষ থাকে তাই উত্তর।
283+928+500=1711 কে 1000 দিয়ে ভাগ দিলে ভাগশেষ 711
নির্ণেয় উত্তর 711

[ferojkabirnh9]

@Arko_1729 give the 3^{rd} problem

[Arko_1729]

Problem 3

যদি n একটা ধনাত্মক পূর্নসংখ্যা হয়, তাহলে n/n+675 কে কাটাকাটি করে লঘিষ্ঠ আকারে লিখলে p/q হয়।
(q-p) এর সম্ভাব্য সকল ভিন্ন ভিন্ন মানের যোগফল কত?

একটি ভগ্নাংশকে কাটাকাটি করলে আমরা হর ও লবকে তাদের গসাগু দিয়ে ভাগ দিই।কাটাকাটির পর লব এবং হরের সাধারণ গুনিতক 1 হয়।

BdMO 2020 national primary

[ferojkabirnh9]

Problem 4
Let be a convex quadrilateral with , , and let be the intersection point of its diagonals. Prove that if and only if .

Last date of posting answer is 13/03/2023 at
12:00 p.m.

Source

IMO 2007

[ferojkabirnh9]

Problem 4
Solution 1

Let and . Then by the isosceles triangles manifest in the figure we have and , so and . Furthermore and .

If , then . But also , so by SSA “Incongruence” (aka. the Law of Sines:

) we have . This translates into , or , which incidentally equals , as desired.

If , then also

by the Exterior Angle Theorem, so and hence and are supplementary. A simple Law of Sines calculation then gives , as desired. This completes both directions of the proof.

Solution 2

Since , , and similarly, . Since , by considering triangles we have

. It follows that .

Now, by the Law of Sines,

.

It follows that if and only if

.

Since ,

,

and

.

From these inequalities, we see that if and only if (i.e., ) or (i.e., ). But if , then triangles are congruent and , a contradiction. Thus we conclude that if and only if. \alpha+\beta =\cfrac{\pi}{3} Q.E.D.

[Pial-age_what]

Problem 5
Let and be circles of radius 1 that are in the same plane and tangent to each other. How many circles of radius 3 are in this plane and tangent to both and ?)

• A. 2
• B.4
• C. 5
• D.6
• E. 8

Last date of replying answer 18/03/23

[ferojkabirnh9]

Ok. There are 5 winners.

[ferojkabirnh9]

Problem 5
Solution

There are two radius 3 circles to which and are both externally tangent. One touches the tops of and and extends upward, and the other the other touches the bottoms and extends downward. There are also two radius 3 circles to which and are both internally tangent, one touching the tops and encircling downward, and the other touching the bottoms and encircling upward. There are two radius 3 circles passing through the point where and are tangent. For one is internally tangent and is externally tangent, and for the other is externally tangent and is internally tangent.

Source

AIME QUESTION SOLUTION.

[ferojkabirnh9]

Problem 6
রাহুল স্থানাংক তলে (3,3) বিন্দুতে আছে। সে একধাপে হয় তার বিন্দুর একঘর উপরের বিন্দুতে যেতে পারে অথবা একঘর ডানের বিন্দুতে যেতে পারে। তার মৌলিক সংখ্যা খুবই পছন্দ, তাই সে কখনো এমন কোনো বিন্দুতে যাবে না যার ভুজ আর কোটি উভয়ই যৌগিক। সে কতভাবে (20,13) বিন্দুতে পৌঁছাতে পারে?

---

Rahul is at (3,3) on the coordinate plane. In each step, he can move one point up or one point to the right. He loves primes, and will never visit a coordinate point where both values are composite. In how many ways can he reach (20,13) ?