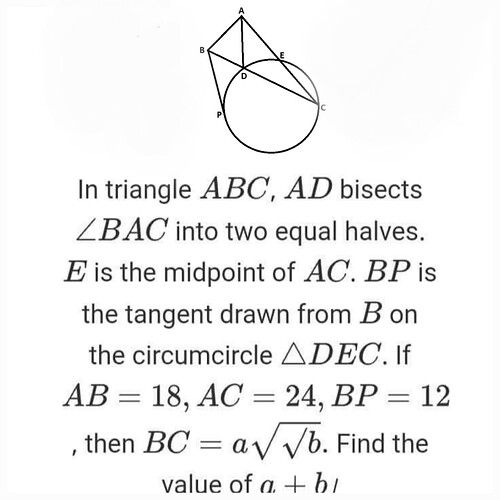
Can someone provide the correct solution for the following problem? I tried to solve it with power of point theorem but keep seeing different answers from different people.
I got 21\sqrt 3 and I didnt get any 1/4th power answer
Isn’t the answer \boxed{445} for a+b format?
I think the answer should be 4 \sqrt{21} . And then, 4\sqrt{\sqrt{21^{2}}} fits the given a\sqrt{\sqrt{b}} format.
Given,
In \triangle ABC, AD bisects \angle BAC into two equal halves, AB=18, AC=24,
BP=12.
We get, \frac{BD}{DC} = \frac{AB}{AC}.
Now,
{{\frac{DC}{BD} =\frac{AC}{AB}}}
\implies \frac{DC}{BD}=\frac{24}{18}
\implies\frac{DC+BD}{BD}=\frac{24+18}{18}
\implies \frac{BC}{BD}=\frac{7}{3}
Now, by using power of a point for circumcircle of \triangle DEC, we get,
BP^2=BD\cdot BC
\implies BD\cdot BC=144
\implies \frac{3BC}{7} \cdot BC=144
\implies BC= \sqrt{144 \cdot \frac{7}{3}}
\implies BC=4 \sqrt{21}
\therefore \boxed{BC=4 \sqrt{21}}
(Please let me know if there is any mistake)